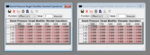
Also, correct me if you guys found different but the high and low range on these tables are 0.000 to 2.032
New boost control XDF tables
- Thread starter carabuser
- Start date
0-1.999999991808 per DAMOS conversion, but the conversion you use, how many decimal places or rounding off determines what you will see in xdf. Hex is the only true value. Converted values may be marginally different in xdfs if everyone uses slightly different conversions, but FFFF is the real max (unsigned) no matter what decimal value it's converted to.
I originally set it to FFFF and saw 2.0. I got curious and extended the high range to 100 for the table and put arbitrary value in. I put a 5 in one of the cells , saved it and opened the table back up and it showed 2.032 (999A). We'll never run a value like this but i wanted to see what it would show. Perhaps you hex guys can educate.
Something went wrong if you're talking about that happening on divisor tables. If a 2 byte FFFF is converted to be equal to 1.9999, you coud put 1,000,000 or 5 in the xdf and it will max at FFFF value no matter how high the xdf limits are set. 999A = 2.032 would be a conversion of about 0.000051676. Correct factor on the divisor Z cells is 0.000030517578 or 0.000031 for short.
Conversion rounding output differences:
FFFF * 0.000030517578 = 1.999999991808
FFFF * 0.00003052 = 2.00015872
FFFF * 0.000031 = 2.031616
That last one would be 2.032 when limited to 3 places in TP, exactly what max hex would be and exactly what you said you saw. If the conversion in the definition you have is 0.000031, either the hex wasn't accurately displayed or you accidentally looked at a different cell/table, but the conversion value you was correct for FFFF.
@RSL, I figured out what i did. On the IJE0S and INA0S tables above, the conversion factor for the Z data is X*0.000030517578. On the IKM0S ROM attached above, the conversion factor in the defined tables is X*0.000031.
Im wondering if we should update the conversion factor for the IKM0S ROM to make it standard across all ROM's....
Ive attached a pic with the values with an updated conversion.
Attachments
Last edited:
Just depends who's defining and if they truncate/round early. For me, depends how lazy I am at the time and how big the XDF is getting. As you can see above, they're all FFFF, the converted value just slightly changes depending how far out it goes. For comparison purposes, the same yardstick should be used, but difference out to the hundredths or greater isn't going to make any real world difference on these. If the XDF were limited to 1-2 places displayed, the conversion place count is even less noticeable.
If the IKM0S is 0.000031, I'll update to the full factor for the sake of matching.
Edit: changed XDF conversion.
Last edited:
so how does the Ikmos 1M ROM deal with the potential detonation caused by the faster onset of boost?
First the throttle delay table and now this.
It’s yet another reason why I want it IKMOS ROM for my car
First the throttle delay table and now this.
It’s yet another reason why I want it IKMOS ROM for my car
You can see why Im confused here. @all4bspinnin is saying that by using the 1M values the car will make 19+ psi extremely quickly.. whereas you’re saying regardless the values are maxed at spool. Who should I believe ?
That's because often people conflate information regarding tunes. This is seen a lot with tune reviews, it's been that way since the Procede vs JB3 days.
You can see it with the MHD OTS maps. Wedge will make some minor changes to a map and release an update, changes that will likely make no discernable difference. People will then start posting threads about how much more or less power their car makes based on scientific measurements like the famous butt dyno or by how much wheels spin they get or even worse all the comments about how "smooth" everything is. Then people start to correlate other peoples misinformation with their own set of unrelated problems and the spread of misinformation snowballs into superstition. Look at all the threads about the burble mod causing turbo damage for instance.
In reality there's four things that will make a difference in the tune relating to spool speed. Timing, WGDC, VANOS and fuel. So unless you've changed any of those factors your not going to spool any faster.
You can see it with the MHD OTS maps. Wedge will make some minor changes to a map and release an update, changes that will likely make no discernable difference. People will then start posting threads about how much more or less power their car makes based on scientific measurements like the famous butt dyno or by how much wheels spin they get or even worse all the comments about how "smooth" everything is. Then people start to correlate other peoples misinformation with their own set of unrelated problems and the spread of misinformation snowballs into superstition. Look at all the threads about the burble mod causing turbo damage for instance.
In reality there's four things that will make a difference in the tune relating to spool speed. Timing, WGDC, VANOS and fuel. So unless you've changed any of those factors your not going to spool any faster.
Tough crowd in here lol. Im not the best at explaining things over the net sometimes.
What im trying to say is the 1m allows for the car to have a higher boost target ceiling at a lower load potentially due to those tables... I need to test to confirm. On the i8/Ij/In ROMs, you'll get a boost target dip like in the first post of this thread. That dip isnt present on a 1m allowing it to hit higher boost levels earlier without throttle closure.
Ive had a 1M make 21psi in only 300 rpms going WOT at 2396 RPM. I cant remember another ROM ive tuned that allowed that much boost at such a low rpm. All other factors were the same - wgdc, PID, load ceiling, fuel, timing, and vanos, etc. Again, I dont advise loading the car up at that low of an RPM. I'm just sharing an observation from experience.
What im trying to say is the 1m allows for the car to have a higher boost target ceiling at a lower load potentially due to those tables... I need to test to confirm. On the i8/Ij/In ROMs, you'll get a boost target dip like in the first post of this thread. That dip isnt present on a 1m allowing it to hit higher boost levels earlier without throttle closure.
Ive had a 1M make 21psi in only 300 rpms going WOT at 2396 RPM. I cant remember another ROM ive tuned that allowed that much boost at such a low rpm. All other factors were the same - wgdc, PID, load ceiling, fuel, timing, and vanos, etc. Again, I dont advise loading the car up at that low of an RPM. I'm just sharing an observation from experience.
Last edited:
The cause of restricted boost targets at lower RPMs will be caused by volumetric efficiency tables. The 1M has lower values in the Boost Request Offset table which is probably what allows you to target more lower down. Same story with the other high output N54 bins.
I've been lazy, but would save a lot of space and any conversion variation. I'll go back and do a find/replace on all multis at some point.Get the decimal places out of here and use X/32768
