I'm working on a DIY tune, and have read the DIY tuning on this forum and Anjuna's N55 tuning on the E90 forum, and could use some help understanding the axis values on the WGDC PID factor tables. I know the P factor X axis is airflow but not sure what the Y axis is, it ranges from -0.125 to +0.188. The I factor table has RPM as the Y axis but again the X axis ranges from -.200 to +.400. The D factor table has X axis of -.028 to +.017 and Y range is -.313 to +.188. What I've read is the numbers that are not RPM and MAF are "error" but haven't found what that means. Is that a count of errors from a certain point? Is it an error number thrown by the DME code? Before I start to "tune" these tables I'm hoping to understand the values, rather than having to change a value, either the axis or cell value, and reviewing the result in the log. I'm taking the PID method approach to tuning my E series N55.
Need help understanding the PID tables in an MHD tune.
- Thread starter JPuehl
- Start date
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
I did some more reading and found that the input to the PID controller is set-point (SP) - process-value (PV). Set-point may be in our logs as either "Boost set-point" or "Boost setpoint factor", I believe "boost setpoint factor" is an axis on many tables, although the logs values for both of those a very low values. It seems to figure out the PID value we either need the PV, assuming boost setpoint or boost setpoint factor is the SP value, or the result of SP - PV.
If using the "WGDC after pid" - "WGDC base" = PID value, I end up with a negative value for example 46.62 (after pid) - 48.4 (base) = -1.78. setpoint factor = 2.61 and setpoint limit = 1.78. This is during an area where I'm below target.
If using the "WGDC after pid" - "WGDC base" = PID value, I end up with a negative value for example 46.62 (after pid) - 48.4 (base) = -1.78. setpoint factor = 2.61 and setpoint limit = 1.78. This is during an area where I'm below target.
from what I understand is, the PV you are looking for isnt in the logs, zero out PID, tune the compressor table to get the boost close to target, then add the stock values to P and D tables, I factor remains 0, WGDC adder for WG spring table must also be 0. make sure when P and D are being used that the comptessor after p-d does not drop below comppressor base.
log P and D and the PV should make sense, hope this helps
log P and D and the PV should make sense, hope this helps
Coming from my professional background, P=proportional, I = integral and D = Derivative, all three are used to tune the speed and intensity of electronic controllers.
Definition = A PID controller is an instrument used in industrial control applications to regulate temperature, flow, pressure, speed and other process variables. PID (proportional integral derivative) controllers use a control loop feedback mechanism to control process variables and are the most accurate and stable controller .
Definition = A PID controller is an instrument used in industrial control applications to regulate temperature, flow, pressure, speed and other process variables. PID (proportional integral derivative) controllers use a control loop feedback mechanism to control process variables and are the most accurate and stable controller .
Yes, what Dumaurier7 said. Not sure of the specifics of BMW's PID implementation in this DME, but expanding on PID control in general, all 3 of those terms (P, I, and D) are factored based on the deviation between actual process value and the target (error term). Functionally, the effect of those terms is:
P - Bigger values help the process value hit target faster. Too much P can cause over-shoot and ringing (ie process value spikes over target value followed by oscillations)
I - bigger values help to overcome offsets between process and target (ie, if process value flattens out below target, bigger I can push process value up to target)
D - Acts as a dampening factor on the process output (ie if process value is overshooting target, and/or ringing, bigger D will minimize/eliminate the overshoot and/or ringing in the process output)
These terms are factored with the process error (difference between process value and setpoint), so their effect is larger when the difference between actual and target is large. Likewise, their effect is smaller as the error value decreases (actual gets closer to target)
Roughly speaking:
Over-damped = process takes too long to hit target set-point
Critically damped = quickest response without overshooting target and ringing
Under-damped = actual process value overshoots target and rings (oscillates)
P - Bigger values help the process value hit target faster. Too much P can cause over-shoot and ringing (ie process value spikes over target value followed by oscillations)
I - bigger values help to overcome offsets between process and target (ie, if process value flattens out below target, bigger I can push process value up to target)
D - Acts as a dampening factor on the process output (ie if process value is overshooting target, and/or ringing, bigger D will minimize/eliminate the overshoot and/or ringing in the process output)
These terms are factored with the process error (difference between process value and setpoint), so their effect is larger when the difference between actual and target is large. Likewise, their effect is smaller as the error value decreases (actual gets closer to target)
Roughly speaking:
Over-damped = process takes too long to hit target set-point
Critically damped = quickest response without overshooting target and ringing
Under-damped = actual process value overshoots target and rings (oscillates)
Also, kind of a technicality, but it's a bit of an over-simplification to say the terms are factored with the process error; I beleive they're technically factored with the timerate of change of the process error. So fir example, if your process leveled out under target, the time rate of change of process error is zero, even though the actual error is not zero. So more P term doesn't help in that scenario, that's where the I term would come in to eliminate that offset.
Actually, this last part might be slightly incorrect, it might be just the D term that looks at timerate of change; I think P is purly looking at the error term. But regarding practicality of how P, I, and D affect the process should be as described.Also, kind of a technicality, but it's a bit of an over-simplification to say the terms are factored with the process error; I beleive they're technically factored with the timerate of change of the process error. So fir example, if your process leveled out under target, the time rate of change of process error is zero, even though the actual error is not zero. So more P term doesn't help in that scenario, that's where the I term would come in to eliminate that offset.
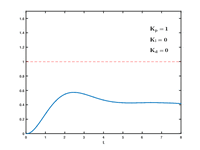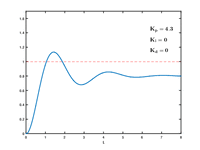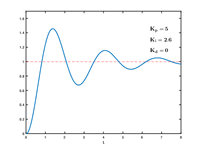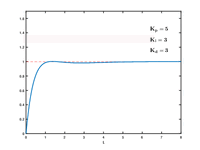
I came acrossa nice GIF illustrating how P, I, and D terms influence response, and thought this would be a good place to drop it for anybody looking onto PID tuning. You can see increasing P gets you near set point sooner (and induces some overshoot & ringing), increasing the I term eliminates the offset (and adds a bit to the overshoot & ringing), then adding more D dampens out the overshoot and ringing.
Attachments
Last edited:
Waking this thread back up... Trying to sort out how to use the following tables.
F30N55 example included below. I'm currently messing with these to sort out what seems to be boost approaching Target too fast on a S63tu engine. Leveraging F30 values to start, it seems to be controlling a very quick to spool engine. Based on the OLS description (above) the last table seems to allow P or D more control on WGDC. Hoping experienced folks can chime in to when and how to use this tables.

| Filter constant for boost pressure deviation (Boost Pressure Deviation (Constant) 4x1) | KL_FK_PLDDIFF |
| Correction factor for filter constant to make filtering fast with high Pld_diff | KL_FK_PLDDIFF_KOR |
| Factor on pilot control up to which the controller with the P and D components can increase the compressor output during operation via pilot control | KL_F_PTURBVST |
F30N55 example included below. I'm currently messing with these to sort out what seems to be boost approaching Target too fast on a S63tu engine. Leveraging F30 values to start, it seems to be controlling a very quick to spool engine. Based on the OLS description (above) the last table seems to allow P or D more control on WGDC. Hoping experienced folks can chime in to when and how to use this tables.
Similar threads
- Replies
- 10
- Views
- 1K
- Replies
- 0
- Views
- 672
- Replies
- 2
- Views
- 2K
- Replies
- 28
- Views
- 2K